What is it for?
When you are fitting a simple time-series regression to your data, you have to make an assumption that indpendent (exogenous) variables in the regression have the same effect on the dependent variable throughout the time of interest. If that’s not true, your regression is likely to be biased in some way. Unfortunately, structural changes in the relationships among variables are common. It might be that government policy changes, a company receives a new tranche of investment, a new treatment is released for a disease you are studying, or whatever. To make modelling decisions in these situations, you must test the assumption of stable regression coefficients over the time series.
Stata includes a command which you can run after fitting a regression on time series data with regress. Just by typing estat sbcusum, you obtain test statistics, critical values at 1, 5 and 10 percent, and a cumulative sum (CUSUM) plot, which shows when and in what way the assumption is broken if it is.
A simple example
Let’s take some data on railway reliability in England, and fit a simple regression. You can download the data file here and the do-file here. The data came from the website of the Office of Rail and Road before being cleaned up and combined with mean temperatures for England in each season, from the Met Office archive. Here are the percentages of journeys delayed or cancelled in London and South-east England for each four-week reporting period from 1997 to 2016:
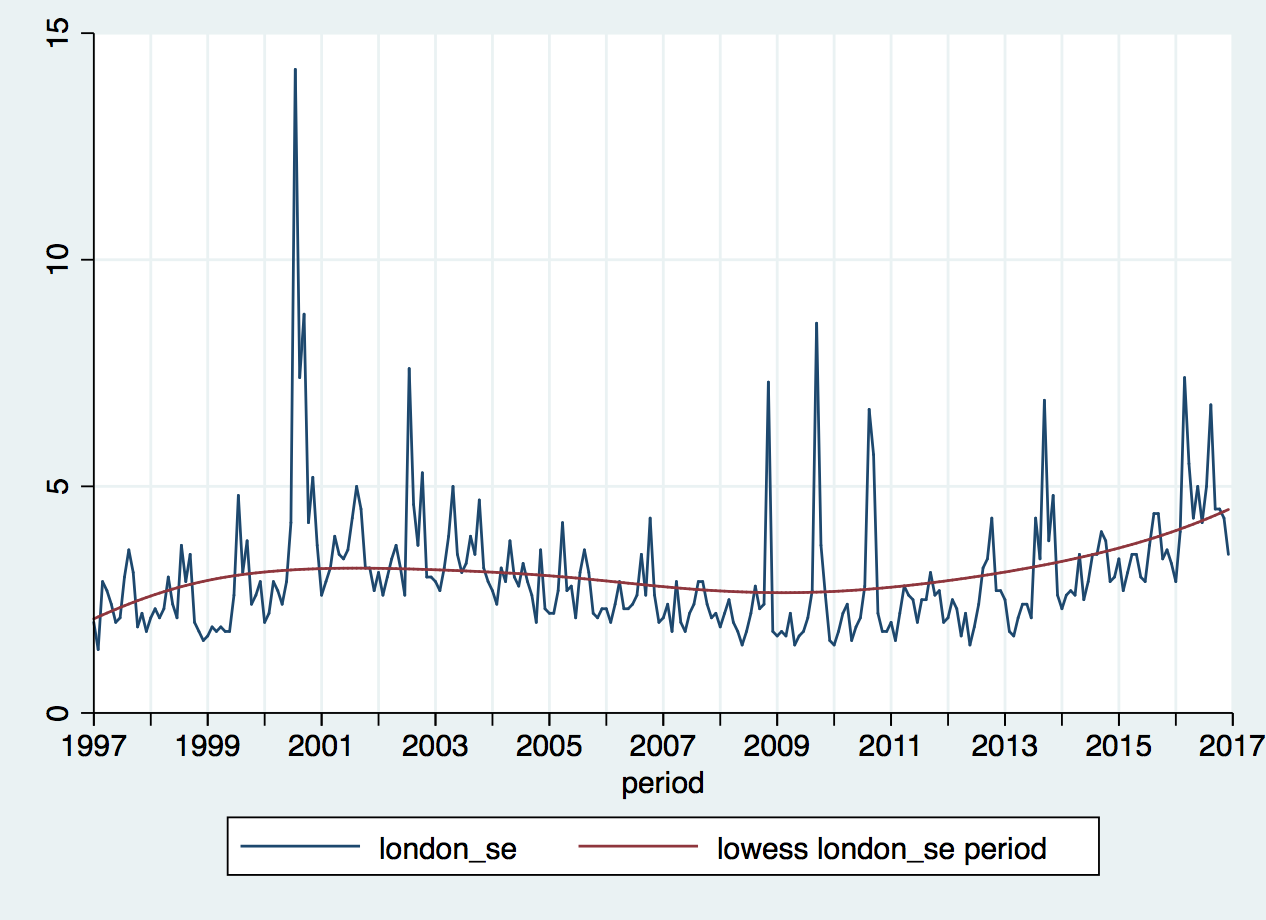
You can see a slow trend that the LOWESS curve picks out: performance got worse, up to about 2003, then got better again, until about 2010, and then got worse again. There’s some sign of seasonality but there are also some large outliers and the percentage, as we might expect, has a skewed distribution. So, one of the first things to do is to calculate a log-transformed version of the dependent variable.
generate logdelay = ln(london_se)
Next, we declare our data to be time series, and use the variable reporting_period as the time variable. Bear in mind that there are thirteen of the four-week reporting periods in each year, and that the years are actually financial years, starting on 6 April and ending on 5 April (this is to do with the British tax system).
tsset reporting_period
Our regression model will account for one period of autoregression, plus the influence of mean temperature. Given that the temperature is averaged across all of England, but the dependent variable is specific to one region, and that the temperature is known for 4 seasons in each year, we might expect it to have a weak effect at best. This is the model-fitting command:
regress logdelay temp L.london_se
Then, when we run estat sbcusum, we get this output and graph:

There is a strong autoregression effect, and a weaker but still significant temperature effect (lower temperatures are associated with more delays).

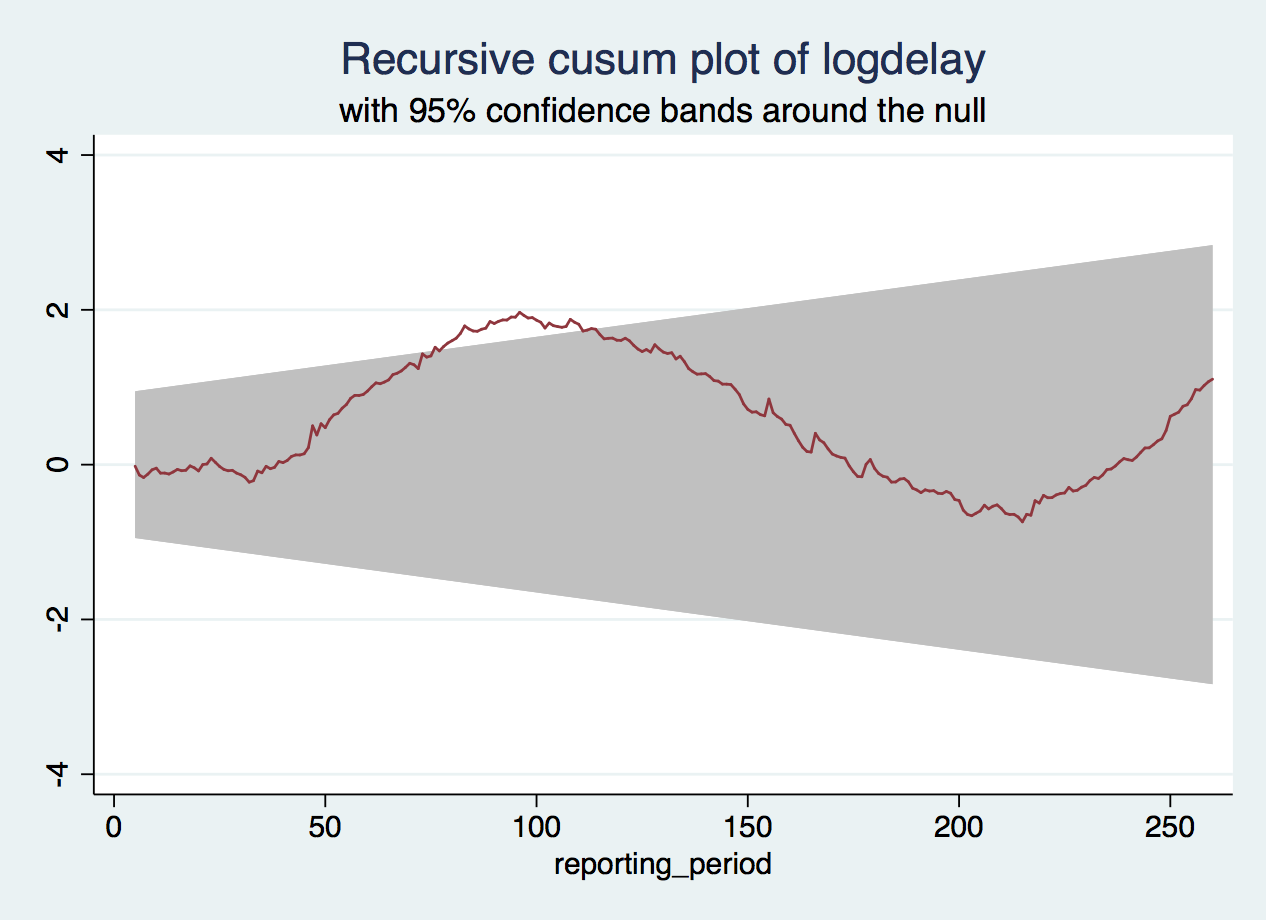
We can see something is wrong because the test statistic is larger than the 1% critical value, and the CUSUM curve extends outside the confidence bands in the plot. The plot also helps us see when this happens, around reporting period 80, which is early 2003 — the same time that we already knew seemed to be a turning point in the long term trend. Also, the CUSUM curve, which we would like to be fairly flat and all contained inside the confidence bands, suddenly, after a promising start, veers upwards from reporting period 50 onwards, which corresponds to the largest spike in the time series, when speed limits were imposed across England following three train crashes. So, the test makes sense in light of the data.
Why is this helpful?
Apart from simply telling us that our simple model is not quite right, it also directs us to when it goes wrong, and in what way. We can look at what we know about the data and the questions we are asking, and revise the model in a sensible way (not just over-fitting).
One thing we can do now is to consider whether it is the temperature coefficient or the lag (autoregression) coefficient that contribute to the departure from stability. We try a model containing only temperature:
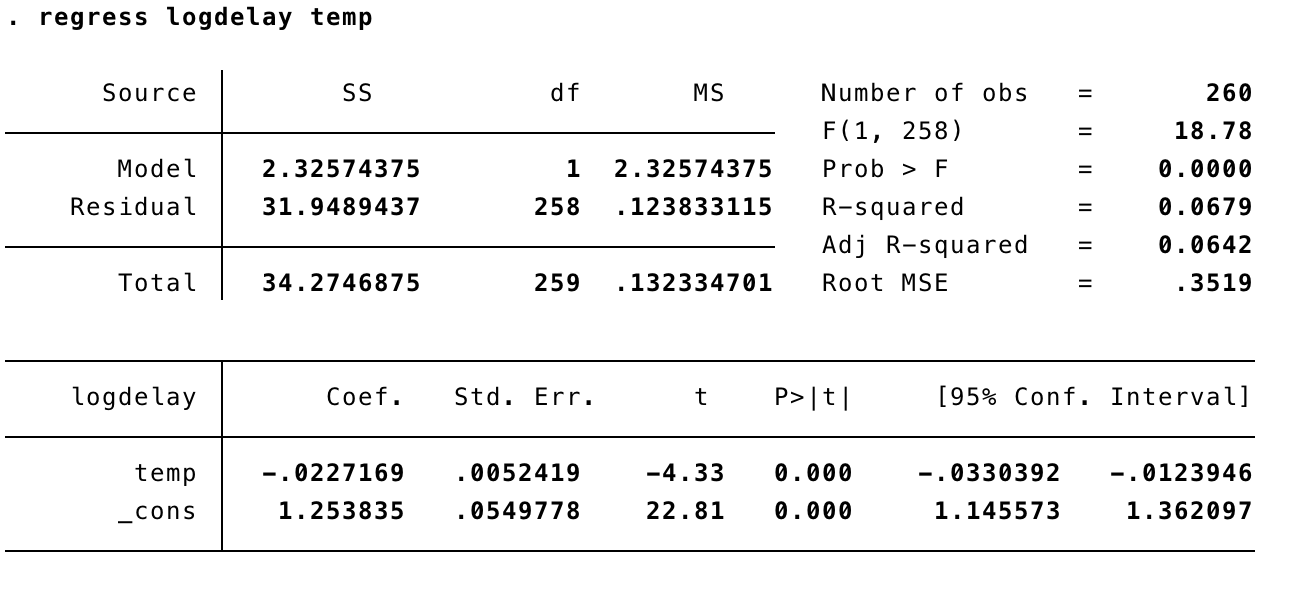

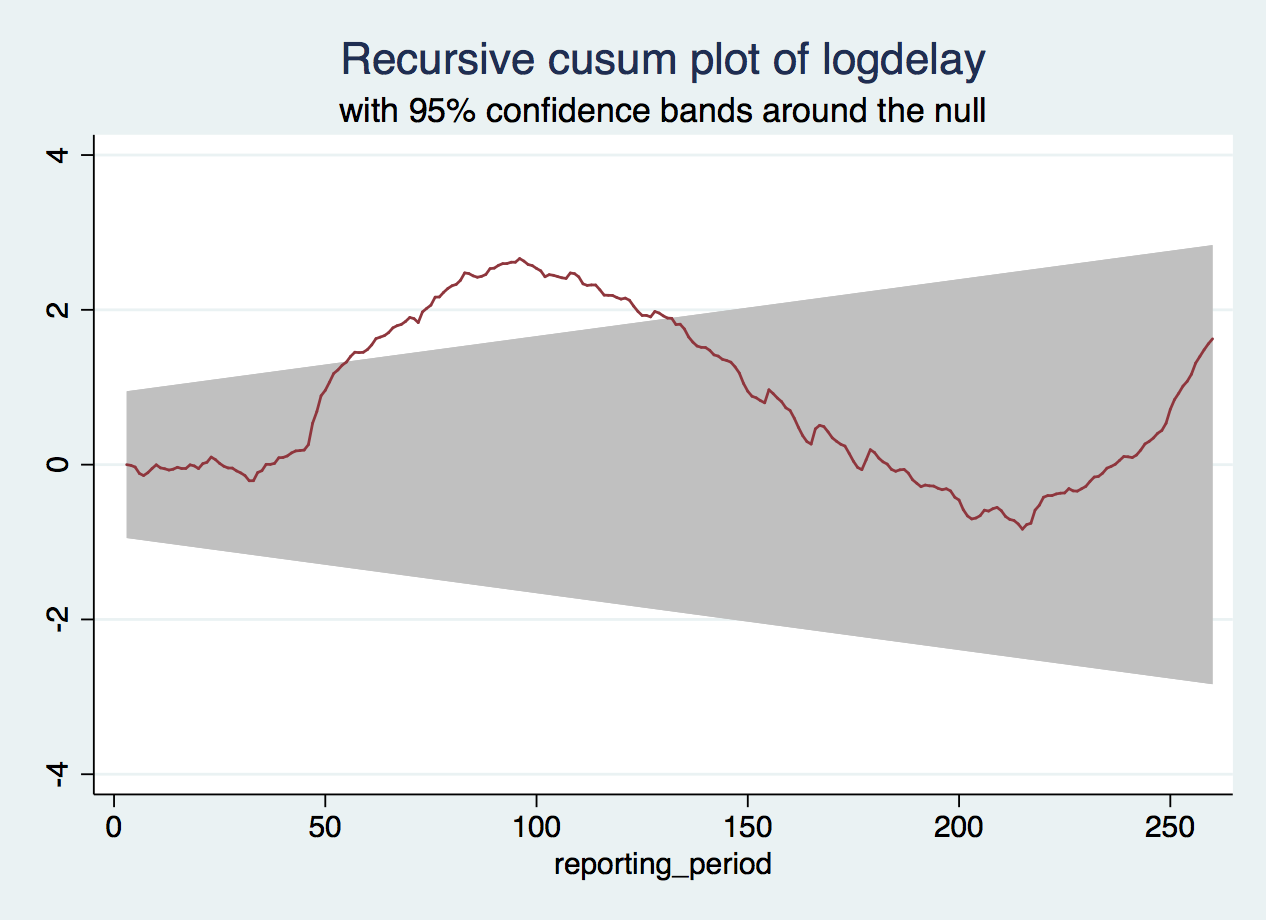
Then one containing only the autoregressive effect:
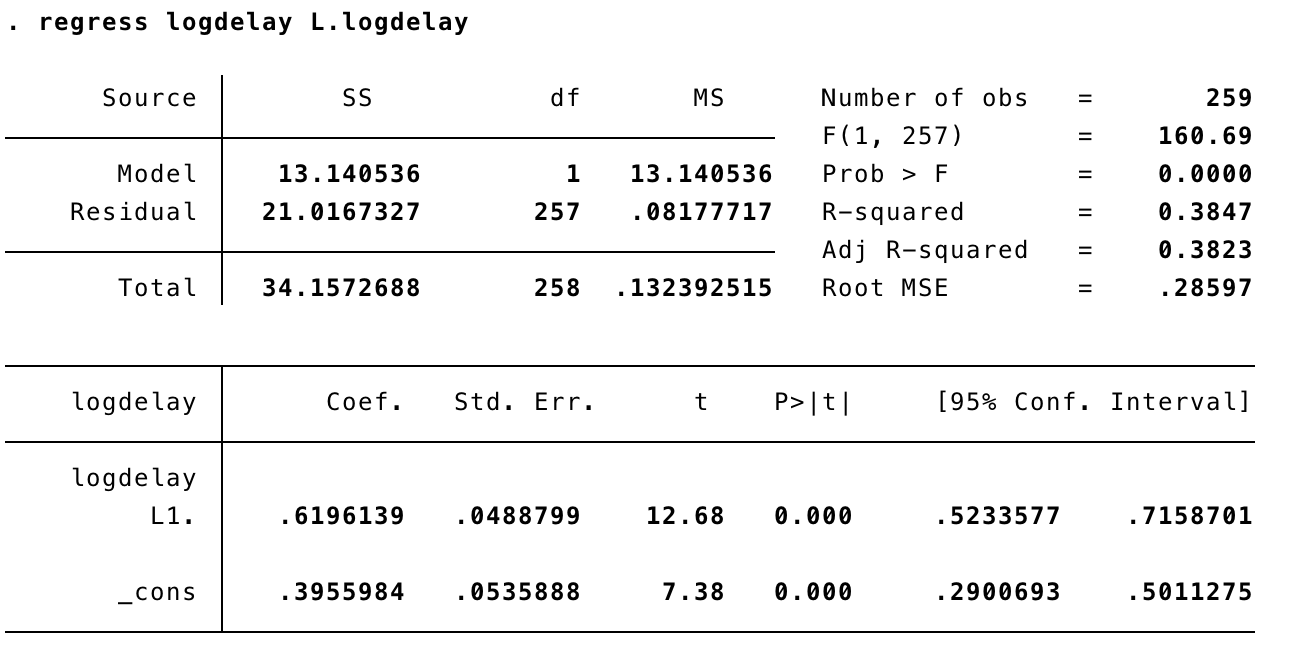

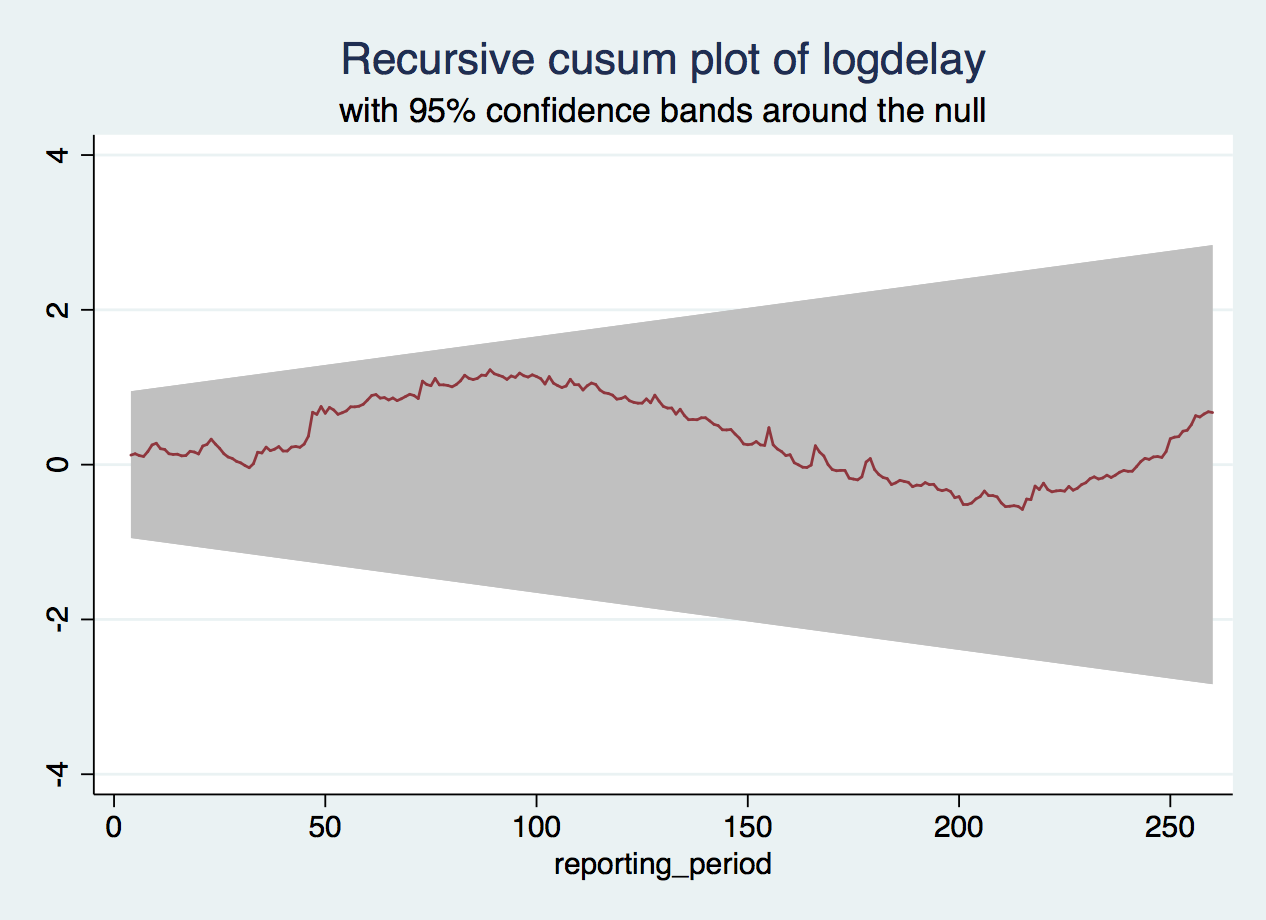
So, temperature seems to be the culprit. Why is this? Without claiming to be any more of an expert on railway matters than any other commuter, there may be a change at around 2001-2003 because autumn leaves used to be blamed for many delays, but around this time, new equipment was deployed to clear the railway lines of these fallen leaves. It is not conclusive, but it does seem that the worst delays each year shift from autumn to winter. Perhaps temperature is more predictive of problems since 2003 because it was masked by other seasonal problems before that. What a lot we can find out from just one test!
Here are the predicted and observed values from our temperature and autorgression model:
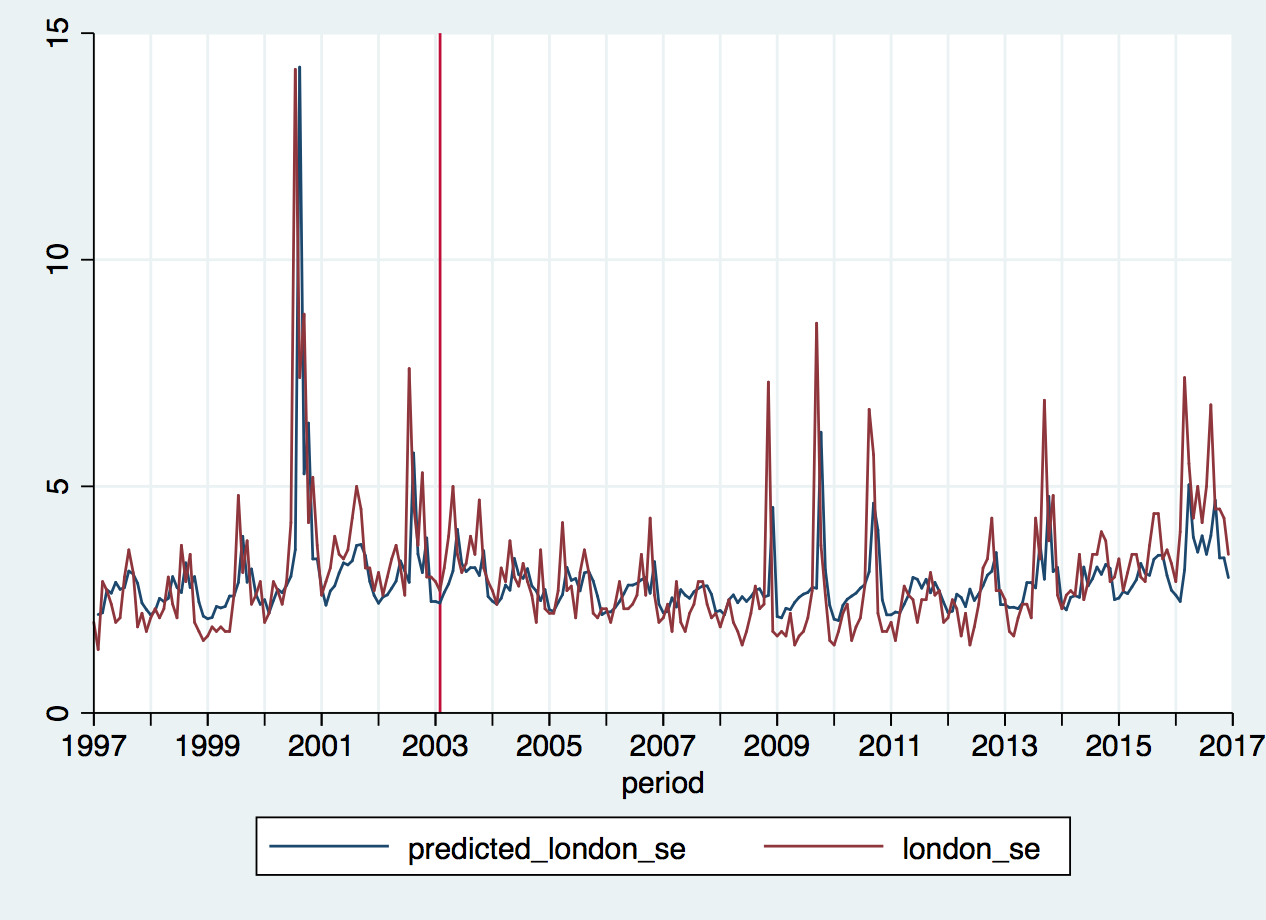
Because temperature is a much weaker predictor than the lagged dependent variable, the change around 2001-2003 is not apparent here. It takes a specialised test and plots to identify it.